- Головна сторінка
- Новини
- Каталог статей
- Конспекти уроків з математики
- Конспекти уроків з інформатики
- Залишити коментар про сайт
| Математика [22] |
| Інформатика [7] |
| Цікавинки науки [16] |
| Виховні години [35] |
| Головна » Файли » Цікавинки науки |
| У категорії матеріалів: 16 Показано матеріалів: 1-10 |
Сторінки: 1 2 » |
Сортувати за: Даті · Назві · Рейтингу · Коментарям · Завантаженням · Переглядам
Наукові керівники: Кикоть В.М., Кислюк О.О.
Зовсім не багато сучасних учнів можуть пояснити, як держава багатіє і чому погано віддавати землі в заставу. Ці питання цікавлять і мене. А оскільки, я дуже люблю математику, то вирішила поєднати приємне з корисним. Таким чином виникла тема «Математичні моделі в задачах з економіки».
Отже, об’єктом дослідження є прикладні задачі економічного змісту, застосування математичних моделей до їх розв’язування.
Мета роботи – систематизувати задачі економічного змісту, які розв’язуються створенням математичних моделей.
Для реалізації поставленої мети необхідно виконати наступні завдання:
- з’ясувати, які існують математичні методи, що застосовуються до розв’язання економічних задач;
- систематизувати теоретичні відомості та методи розв’язання економічних задач;
- визначити найбільш раціональні методи розв’язування економічних задач;
- розглянути різні типи прикладних задач економічного змісту;
- запропонувати банк задач для розглядання їх на уроках, гуртках, факультативах за різними методами їх розв’язання.
Актуальність наукової роботи обумовлюється показом можливостей використання математичних моделей при розв’язуванні задач з економіки.
При написанні застосовано теоретичні та емпіричні методи: метод моделювання, аналіз та синтез, порівняння, абстрагування, уявний експеримент.
Наукова новизна роботи полягає у розв’язуванні економічних задач за допомогою різноманітних математичних моделей.
Практичне значення нашої роботи полягає в тому, що дослідження обраної теми доповнює наукові знання з математики та економіки, розширює математичний кругозір, допомагає у підготовці до самостійного життя. Дана робота може бути використана учнями, а також вчителями математики на факультативах, гуртках, спецкурсах.
В основу роботи покладені матеріали, які використовують математичне моделювання і математичні методи розв’язування економічних задач.
При розв’язанні задач за допомогою математичного моделювання доцільно виділити три етапи:
1. Створення математичної моделі даної задачі.
2. Розв’язання відповідної математичної моделі.
3. Аналіз відповіді.
В роботі розглянуто задачі на різні види економічно діяльності:
1. Задачі на знаходження оптимальних рішень,
2. Задачі на банківську діяльність,
3. Задачі на цінні папери,
4. Задачі на сімейний бюджет,
5. Задачі на страхування.
- Категория: Цікавинки науки
- Добавил: Ольга
- Дата: 27.12.2014
- Категория: Цікавинки науки
- Добавил: Ольга
- Дата: 30.11.2014
Тези
Використання прийомів і методів розвивального навчання
Можливість суттєвих змін у школі теоретики і практики вітчизняної освіти пов’язують з ідеями розвивального навчання.
Актуальність дослідження обумовлена тим, що українське суспільство на сучасному етапі розвитку має особливо гостру потребу в самостійних, відповідальних, творчих особистостях, що усвідомлюють свою суб’єктність. Серед ряду сучасних освітніх технологій в своїй професійній практиці віддаю перевагу розвивальному навчанню.
Звичайно, дитині і в традиційній школі приємно усвідомлювати, що вона відповідає правильно, але, якщо точність відповіді ґрунтується лише на механічному запам’ятовуванні, це не приносить істинної радості пізнання. Ми лише тоді відчуваємо справжнє задоволення, коли наша правота є результатом самостійних роздумів, особистої думки і прийняття відповідного рішення.
Реалізація такого підходу до навчання, при якому дитина живе з відчуттям хоч маленького, але особистого успіху, відчуваючи при цьому і впевненість в собі, складає суть розвивального навчання – потреба дитини в любові, в почутті власної гідності, в відчутті значимості особистісного «Я», почуття впевненості в своїх силах і позитивній оцінці зі сторони оточуючих – тобто відчуття себе особистістю. Отож, розвивальне навчання спрямоване на виховання і розвиток особистості дитини та формування не лише конкретного, а й теоретичного мислення. Цей процес здійснюється завдяки дослідницькому методу навчання – квазідослідницькому, коли поняття задаються не в готовому вигляді, не в формі визначень чи правил. Дитина повторює в процесі вивчення хід і результати відповідного наукового дослідження, вона стає маленьким вченим, який робить своє власне відкриття.
Майстерність учителя полягає, по-перше, в умінні створити такі навчальні ситуації, коли у дитини з’являється потреба в пошуку способу дії, тоді дитина стоїть на межі між знанням і незнанням; по-друге, в організації співробітництва дітей, в ході якого і відбувається відкриття і засвоєння понять; по-третє, в можливості організувати, направляти і підтримувати змістовний навчальний діалог між дітьми. Це можливе лише тоді, коли вчитель сам займає позицію учня, чиї висловлювання, ідеї теж можуть піддатися критиці, як і дітей.
В системі розвивального навчання є своя типологія і структура уроків.
1. Створення ситуації успіху – оцінка попереднього способу дії і того, чи вміємо ним користуватися .
2. Створення ситуації розриву – пропонується завдання, зовні схоже на попереднє, але в корені – ні.
3. Аналіз умов – аналіз того, що було в попередньому способі, що дозволяло нам виконувати завдання, а зараз – ні.
4. Постановка навчальної задачі. Учитель підводить дітей до моменту, що вони самі формулюють навчальну задачу: «Треба знайти такий спосіб, щоб можна було…». Цю задачу фіксують коротко і стисло у модельній формі (знаковій чи графічній). Це є міст до наступного уроку або етапу уроку.
5. Аналіз умов рішення задач, щоб знайти, відкрити новий спосіб дії.
6. Моделювання і перетворення моделі.
7. Контроль способу – перевірка на практиці відкритого способу.
8. Оцінка способу – як я та інші вміють користуватися відкритим способом.
З цих етапів випливають і різні типи уроків:
• Постановки навчальної задачі.
• Аналіз умов, рішення задачі, моделювання відкритого способу.
• Моделювання способу.
• Постановки і рішення навчальної задачі.
• Рішення конкретно-практичних задач.
• Урок контролю і оцінки способу.
- Категория: Цікавинки науки
- Добавил: Ольга
- Дата: 02.11.2014
АКТУАЛЬНІ ПРОБЛЕМИ ФУНДАМЕНТАЛЬНОЇ І ПРИКЛАДНОЇ МАТЕМАТИКИ
Сучасні потреби розвитку України вимагають переходу на нову, більш гнучку, ніж існуюча, стратегію математичної освіти. Особистісна спрямованість освіти є однією з основних тенденцій розвитку сучасної школи. Повернення школи до особистості учня виступає провідним принципом нового педагогічного мислення. І це не випадково. Суспільству потрібна компетентна, творча особистість, яка здатна брати активну участь у розвитку сучасного виробництва, економіки, науки та культури. Саме тому на перший план шкільної освіти виходить завдання створення оптимально сприятливих умов для виявлення і розвитку здібностей учнів, задоволення їхніх інтересів і потреб, розвиток навчально-пізнавальної активності та творчої самостійності. [1]
Уже сьогодні перед вищою школою стоїть завдання побудови системи освіти таким чином, щоб не тільки підготувати з молодої людини фахівця, але й закласти в нього розуміння необхідності навчатись, самовдосконалюватись протягом всього життя. Адже освіта формує особистість у всій її багатовимірності, а не просто дає знання і професію.
Прикладна математика — галузь математики, що розглядає застосування математичних знань в інших сферах діяльності. [2]
- Категория: Цікавинки науки
- Добавил: Ольга
- Дата: 02.11.2014
Наукова робота "Особливості стратегії гри"
Цікавими й популярними в математиці стають задачі на ігри двох або кількох осіб. Щоб розв’язати таку задачу потрібно мінімум математичних знань, але потрібно мати досить розвинене логічне мислення.
Гра має важливе значення в філософії, педагогіці, культурології, зустрічається в релігієзнавстві тощо, але найбільш детально і фундаментально вона розглядається в математичному моделюванні. Саме завдяки математичним моделям найлегше зрозуміти призначення та сутність гри. Щодо досліджень в цій сфері, то вони є дуже обмежені, особливо в шкільному курсі математики, хоча зараз в олімпіадах різного рівня задачі на стратегію гри зустрічаються все частіше. Саме цим визначається актуальність нашого дослідження.
Теорія ігор – теорія математичних моделей прийняття оптимальних рішень в умовах конфлікту, намагається математично зафіксувати поведінку в стратегічних ситуаціях, в яких успіх суб’єкта, що робить вибір залежить від вибору інших учасників.
Отже, вивчаючи теорію гри, ми дослідити теоретичні основи теорії ігор та визначити окремі засади її практичного використання на конкретних прикладах, тобто суть розв’язання задачі на ігри двох осіб. Дані задачі ми розподілили на класи та показали їхнє практичне застосування не тільки на уроках математики, але й в житті.
Хоча при використанні стратегії гри результат у деякій мірі залежить від випадковостей, але багато що визначається й майстерністю суперників. Успішна гра потребує точних математичних розрахунків. Саме тому вибрана нами тема є актуальною.
- Категория: Цікавинки науки
- Добавил: Ольга
- Дата: 19.10.2014
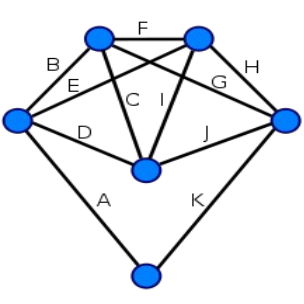
Наукова робота "Розвязування системи рівнянь за допомогою графів"
У наш час граф стає однією з найпоширеніших і найпопулярніших математичних моделей у багатьох сферах науки і техніки. Картинка у вигляді набору точок на площині та ліній, проведених між деякими з них, стала зручною і наочною формою зображення найрізноманітніших об’єктів, процесів та явищ.
Актуальність нашої роботи полягає в тому, що на даний момент теорія графів все ширше застосовується в різноманітних сферах нашої життєдіяльності.
Вивчаючи теорію графів, ми поставили таку мету: навчитись застосовувати графи для розв’язування системи рівнянь, тематика яких є актуальною в нинішньому суспільстві.
Дослідження показало, що розглянутий спосіб розв’язування систем лінійних рівнянь:
1) розвиває творчу активність учнів та формує в них потребу постійно розширювати та поглиблювати свої знання;
2) розширює математичну культуру учнів і демонструє наявність нетрадиційних підходів до розв’язування математичних задач;
3) удосконалює прийоми розумової діяльності учнів і розвиває в них дослідницький, творчий підхід до постановки і розв’язування задач у різних сфер людської діяльності.
Працюючи над роботою, ми зрозуміли, що дана тема є актуальною і перспективною в наш час.
- Категория: Цікавинки науки
- Добавил: Ольга
- Дата: 19.10.2014
- Категория: Цікавинки науки
- Добавил: Ольга
- Дата: 19.10.2014
Календарне планування уроків математики з обдарованими учнями 6 клас
Розробки занять
1. Розв’язування елементарних задач на логічне мислення та задач на сірниках
2. Розв’язування задач-жартів та задач-загадків
7. Розв’язування задач на відновлення запису в прикладах на додавання, віднімання, множення
- Категория: Цікавинки науки
- Добавил: Ольга
- Дата: 11.10.2014
- Категория: Цікавинки науки
- Добавил: Ольга
- Дата: 11.10.2014